La logica ontologica: seconda parte
-
Cristian Rossi
- 25 Aug, 2023
- 18 Mins read

La logica formale per come è stata concepita è completamente sbagliata, si fonda sul principio di identità, che a sua volta ammette che l'essere sia un genere. Inoltre il principio del terzo escluso tratta verità e menzogna come contraddittori, ritenendo sia la verità che la menzogna generi a cui partecipare. L'unico principio buono della logica formale è il principio di non contraddizione. Una soluzione, anch'essa sbagliata, a questo problema, è concepire l'ente come un genere e la verità e la menzogna come estremi di due opposti, quindi come contrari e non contraddittori. In sintesi questa è la formalizzazione logica del pensiero di Meinong. Per chi non lo sapesse, la logica formale, rispetto a quella classica aggiunge i quantificatori, che sono:
- Esiste.
- Non esiste.
- Per ogni (o tutti gli).
- Per ogni con il not, che ha come valore il medesimo di esiste.
Dico così perché i sillogismi sono già logica predicativa. La proposizionale è priva di quantificatori. A è B, è la logica proposizionale. Quale A è B è la logica predicativa. La differenza è che la prima non ha i quantificatori, la seconda sì, la prima ha pertanto solo i connettivi verofunzionali, chiamati anche operatori logici, che sono AND (e), OR (o), XOR(ex or), NOT (non), implicazione e doppia implicazione. La prima è più vecchia della seconda nonostante sia più complicata. Poi ci sono le logiche modali e temporali, e molte altre che sono più moderne. La logica formale essendo derivata da quella classica, quella Aristotelica, fornisce una visione dicotomica ed ontificata della realtà: ciascuna teoria viene assunta come un ente generico che può assumere a sua volta un valore di verità, cui viene messo in relazione tramite un connettore verofunzionale più un altro ente. In altre parole, vi sarà già capitato di leggere espressioni come A AND B, per esempio... ecco, i valori sono sempre due: vero e falso. Ma come abbiamo già analizzato anche nei precedenti articoli, la negazione del vero porta a qualcosa di falso, ma la negazione del falso non porta ad un valore vero, ma piuttosto a tutto ciò che non è falso, ossia non vero. Risulterebbe vero infatti dal momento che si fornisse una teoria che asserirebbe una relazione di proprietà, nel senso che "se non è zuppa, è pan bagnato", dove la teoria descrive proprio un campo ristretto di dicotomia tra "zuppa" e "pan bagnato". Persino tra ovvietà di contrari come "caldo" e "freddo" c'è una teoria che ne descrive le differenze, la termodinamica. Ridurre la logica a dei contrari dovrebbe essere pertanto considerata un'aporia, poiché in prima istanza la logica formale viene destinata ad essere trasformata in logica fuzzy dal momento che le variabili sono relativistiche: il caldo è caldo rispetto a qualcosa, non è un valore specifico, ma è una quantità relazionata ad una misura, nel caso di un umano è relazionata alla sua scala sensoriale più la relazione tra la temperatura dell'oggetto e quella dell'organismo. Come seconda motivazione, è un'aporia per il fatto che le esistenze essendo dotate di proprietà, possono presentare una terza, una quarta e persino una quinta via. Per una formalizzazione più matematica, se ho A={a,b,c,d} e vado ad escludere, a negare, c, otterremo non un valore specifico ma un insieme di elementi che potranno essere il valore vero ma a cui noi senza un'ulteriore teoria non potremmo mai risalire. Pertanto la logica che qui propongo è una logica a 3 parametri, anche se in realtà l'analisi è comunque dicotomica perché si divide prima nell'analisi delle presupposizioni esistenziali, in apofantico e non apofantico, e poi nell'apofantico si può distinguere tra vero e falso. La dicotomia cade tuttavia nel momento in cui si va a relazionare il falso con il non apofantico. Ovviamente i riferimenti di questa logica devono essere ontologici e non potrebbero essere altrimenti, dato che non si può discutere di logica se non si prende in causa la dialettica e l'esistenzialità. A tale scopo si può asserire che la doppia negazione di p è non apofantico, perché la negazione è della negazione di p. È come scrivere ¬(¬p), dove "¬" sta per la negazione. Come operatore si può dunque descrivere come doppia negazione, oppure con la lettera greca iota (ι), essendo usata per descrivere i numeri immaginari, ed essendo usata nella logica del secondo ordine per le definizioni definite, usandola pertanto qui per definire questo tipo di negazione: ιp. Potrebbe esserci tuttavia confusione nella formalizzazione matematica, si potrebbe usare ι¬, ma allora tanto vale utilizzare la doppia negazione semplice, che rimane sicuramente la più inutitiva. Dati l'insieme U, l'insieme F e l'insieme T, dove T è sottoinsieme di F ed F è sottoinsieme di U, dove U è universe, T è true e F è false, si può seguire quanto segue per derivare una formalizzazione più completa e dettagliata di quello che ho inteso nelle precedenti righe: Costruiamo un altro insieme distaccato da questi 3 che contiene solo 2 elementi: 0 e 1. Tutti gli elementi che appartengono a U, ma non a F o T non ricevono 0 o 1. Tutti gli elementi che appartengono a U, a F ma non a T ricevono 0. Tutti gli elementi che appartengono a U, F e T ricevono 1. Ora, 0 è falso, 1 è vero e la non assegnazione è il non apofantico.
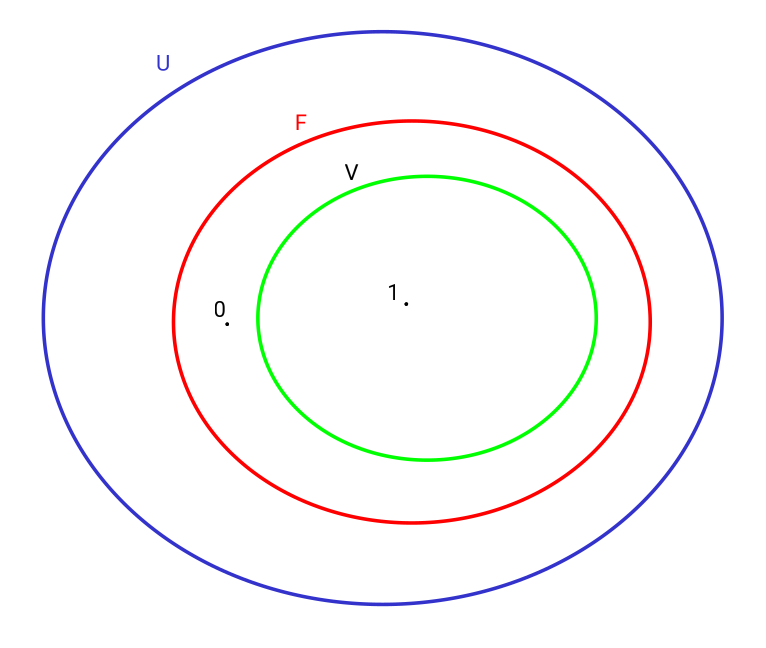
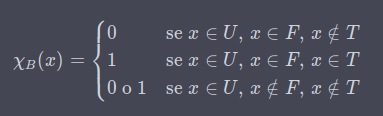
Tutto ciò che è 0 e 1 al contempo e quindi quando i valori non sono stati ancora distribuiti e sono da distribuire, allora si dice che è apofantico. Ma non tutto il non apofantico sarà apofantico. Quando si distingue tra non apofantico e apofantico si stabiliscono i due reami. Non tutto l'apofantico può diventare non apofantico e non tutto il non apofantico può diventare apofantico. In un processo deduttivo ovviamente non si può passare dal non apofantico all'apofantico, ma ciò è possibile quando si aggiungono informazioni che completano l'enunciato, così come è possibile che l'apofantico sia non apofantico riducendo le informazioni (attraverso la negazione di una premessa falsa). La negazione di un non apofantico, è una premessa falsa: ¬F=N ¬N=F
dove per F si intende falso e per N si intende null, nullo, ovvero non apofantico. La negazione stretta potrebbe pertanto essere così semplificata:
"i non non-studenti non sono stati ammessi"
鬬p
La negazione stretta agisce sull'atto stesso, quindi ι¬V dovrebbe essere N, di conseguenza ι¬V=N, mentre ι¬N=V. E la scrittura con la doppia negazione è ovviamente analoga:
¬¬V=N
¬¬F=V
¬¬N=V
Vero è tutto ciò a cui ci si riferisce come aggregato di proprietà ottenuto da una determinata teoria che si presenta come verificabile, mentre falso è tutto ciò che non è quell'aggregato di proprietà. Nullo o non apofantico è tutto ciò che non è falso e che pertanto non è nemmeno vero (e dunque non non vero). Ma perché "stretta"? Perché nega solo l'atto del connettivo logico e non l'intero proposizione, proponendosi come una sorta di micro-operatore, cosa che porta a definire anche il concetto di affermazione stretta, che non necessita di essere formalizzata, in quando la negazione stretta va usata solo nella logica del secondo ordine, cioè quando si dice per esempio ι¬f(x), che si può interpretare come "non si dà il caso che vi sia una proprietà f per le x (che esistono)". Per la negazione semplice invece: ¬f(x) si legge "non si dà il caso che x assegnato ad f esista". È stretta perché funziona quasi come un quantificatore, è un operatore che sta a metà tra la logica predicativa e quella modale e se si riuscisse a costruire un sistema con questa logica si avrebbe una logica completamente ontologica, che è ciò che andrò a dimostrare di avere fatto nei prossimi articoli e con il progetto che sto sviluppando, il cui nome è TheoryFlow .
- ARCHETIPI ONTOLOGICI -
Avendo definito cosa è la negazione e le sue implicazioni sui valori di verità, con tanto di dimostrazione per insiemi e diagrammi di Eulero-Venn, andiamo ora a comprendere più in dettaglio il significato dei connettivi verofunzionali, cioè degli operatori logici. Nella teoria degli insiemi vi sono molte operazioni e può risultare difficoltoso orientarsi per quanto riguarda la correlazione con i connettivi verofunzionali. Pertanto procederò con una prima illustrazione ontologica, per poi porre fondamento neuroscientifico a ciò che poi andrò a definire come archetipi ontologici. Come potrebbe suggerire il nome, questi archetipi non si riferiscono al sé, ma piuttosto all'essere, andando di fatto a costituire una sorta di "inconscio ontologico". L'inconscio collettivo (vedi tesi di Jung) è uno specchio dell'inconscio ontologico; gli archetipi che esso usa per le funzioni e anche la sua simbologia (inflazione e deflazione), derivano da archetipi compiutamente ontologici. Questi archetipi non hanno utilità nella struttura della psiche, ma esistono per il semplice fatto che la psiche è essere. E non servendo a niente, vengono fraintesi. Si pongono a priori rispetto alla matematica, essendo la quantità una questione a posteriori, ponendosi pertanto come più generali di essa. Sono archetipi della pura forma del tempo. Gli archetipi ontologici sono 4, riguardano il tempo e pertanto la storicità dell'essere e sono espansione, estensione, compressione e dissoluzione.
Ad esempio, il tempo si può dissolvere nel presente, nel senso che può sciogliersi e diventare scomponibile. Sono molto fraintendibili, come già detto: l'archetipo dell'espansione può avere due significati opposti, può essere l'espansione dell'essere nel sé con la scomparsa dell'io, ma anche l'espansione della società nel sé con la scomparsa della volontà. Entrambi prendono questo archetipo come modello. Ma in realtà il vero significato è semplicemente qualcosa che semplificia un'altra cosa. Se c'è qualcosa che si espande, allora qualcosa si dissolve.
Tenendo conto della seguente analogia:
- AND → compressione.
- Implicazione → espansione.
- OR → estensione.
- NOT → dissoluzione.
Possiamo ricavare che per ogni implicazione vi sia una dissoluzione, cioè che per ogni implicazione vi sia altresì una proposizione che viene negata. E altresì che da una compressione se ne derivi anche un'estensione: da un AND si ricava un OR. E questi, come già accennato nei precedenti articoli, fondano la storia e pertanto il discorso del logos storico, della narrativa dell'essere. Ho già parlato di pre-tematizzazione, de-tematizzazione e tematizzazione. elementi a loro volta archetipi ontologici. La differenza consta che non hanno una simbologia fissa perché non riguardano il sé e pertanto non hanno alcun canone. Questi archetipi hanno un significato variabile in base al processo. Il 4 negli archetipi dell'inconscio collettivo significa sempre la stessa cosa, mentre gli archetipi ontologici hanno un significato variabile. Ed infatti riguardano la dialettica delle esistenze, dell'essere, in modo diretto. Per questo nelle filosofie ci sono stati molti errori, oltre a quelli della trasposizione del significato sul significante. Ed anzi, questo stesso errore è possibile solo perché è possibile traslare il significato di questi archetipi. Gli errori categorici derivano da un utilizzo equivoco di questi archetipi. Se non saranno loro stessi tematizzati è impossibile uscire fuori dall'errore, è questo che voleva dire Kant. Sono i concetti a priori della dialettica, ed il linguaggio si sviluppa determinandosi su queste "regole". Ma queste regole esistono come logos, possiamo dire che sono il logos stesso e che esso non è solo nella coscienza, ma anche come archetipi ontologici. A differenza degli archetipi comuni, quelli ontologici sono ovunque, come accennato all'inizio di questo articolo, andando a definire appunto come tutto sia logico e come uscire dalla logica sia ancora un passaggio logico, seppur per assurdo. Non stanno solo nell'inconscio collettivo, pervadono tutto, persino quello personale. Sono la dialettica del logos, la grammatica dell'essere. L'errore semplicemente è un inserire contenuti errati, ma di fatto gli elementi sono coerenti con il logos. Hegel stesso parlò di questi archetipi ontologici, o meglio, dei primi due, quelli di compressione ed espansione. Hegel stesso con questo passo parla persino di unicità dialettica deducendola dalla percezione:
Con ciò cade l'ultimo in quanto separava l'esser-per-sé e l'essere per altro. Sotto un unico e medesimo riguardo l'oggetto è piuttosto il contrario di sé stesso: è per sé in quanto è per altro, ed è per altro in quanto è per sé. Esso è per sé, è riflesso in sé stesso, è Uno; ma questo essere per sé, essere riflesso in sé stesso ed essere Uno, è in unità con il contrario, l'esser-per-altro, ed è posto quindi solo come un tolto; o questo esser-per-sé è tanto inessenziale, quanto ciò che solo doveva esser l'inessenziale, vale a dire quanto la relazione verso altro.
Dice che la percezione implicitamente è dialettica perché non può fare a meno di determinare un oggetto e delle proprietà, e quindi implicitamente sa che l'oggetto in realtà non esiste nella sua inseità ma può esistere come tale grazie alla sua dialettica con il tutto. Gli archetipi ontologici non sono lal ogica, ma conferiscono unicamente la temporalità e dunque la storicità all'essere, sono elementi molto generici, ma che corrispondono proprio a delle applicazioni logiche sulla realtà, cosa che permette l'evoluzione dell'essere. I connettivi logici sono l'esplicazione della dialettica tra le proprietà, che sono già in potenza dell'essere. dove l'essere è l'unica istanza possibile dove si possono presentare le proprietà stesse. L'applicazione della negazione sulla realtà per esempio porta ad una dissoluzione. L'espansione doppioimplica la compressione, mentre l'estensione doppioimplica la dissoluzione. Ciò permette di sviluppare una storicità dell'essere e pertanto tra le proprietà stesse che si danno nella teoria. La logica ontologica descrive pertanto la realtà e nel farlo utilizza le relazioni tra le proprietà, nonché gli operatori logici, sui valori di verità di vero, falso e non apofantico. Un altro esempio? Argomentiamo tramite gli archetipi ontologici la relazione tra inconscio e libertà. L'inconscio è stato selezionato per ignorare il concetto di morte per rispondere alla tendenza alla dissoluzione dell'io, che guardacaso, come già detto, si comporta proprio come una negazione. Questo ha portato l'inconscio ad essere molto rigido e a selezionare delle sequenze specifiche di miti in grado di preservare la vita. Ciò ha come effetto collaterale quello di costruire una barriera che separa il cervello dagli stimoli esterni, una sorta di barriera che viene ristabilita come se ci fosse una omeostasi neurale che rende il cervello attivamente indipendente dagli stimoli esterni, andando pertanto a spiegare il fondamento della possibilità della libertà, che comunque consta già nel discorso dialettico dell'essere, ed anzi nella sua potenza rispetto alle relazioni tra proprietà. La logica viene fondata infatti come interazione tra le proprietà, dove una proprietà a può essere messa a confronto con una proprietà b per mezzo dell'unione (OR), andando a formare un insieme, cioè un aggregato di proprietà, di elementi, corrispondenti ad a, oppure b, o entrambi. L'AND essendo una congiunzione, nonché un'intersezione tra le proprietà, genera un aggregato di proprietà che è l'insieme degli elementi presenti nella proprietà a e nella proprietà b. L'implicazione corrisponde al concetto di sottoinsieme in matematica, dove {x|x∈A}⊆{x∣x∈B}}, ovvero dove se a implica b, allora l'insieme dei casi in cui a è vero è un sottoinsieme dell'insieme dei casi in cui b è vero.
La formalizzazione delle correlazioni tra V, F e N, cioè tra vero, falso (e dunque apofantico) e nullo cioè non apofantico, è la seguente:
- x ∈ V and V(x) = vero
- x ∈ A \ V and A(x) = falso
- x ∉ A and x ∉ V = insime vuoto o non apofantico
Dunque:

Da ciò possiamo tra l'altro intuire che se da una parte i connettivi logici sono già fondati nella dialettica come unione o come differenza, due caratteristiche ontologiche che riscontriamo anche negli archetipi ontologici sottoforma di estensione (OR) e compressione (AND), dall'altra troviamo anche che tutte le negazioni attuate sui valori di verità siano in realtà delle proposizioni circa la dialettica di una teoria. Da questo teorema si potrebbero ricavare tutti i valori di verità, tuttavia per risparmiare fatica nelle operazioni logiche, metterò qui di seguito le tavole di verità, includendo i tre valori più l'analogia dei connettivi logici con gli archetipi ontologici.
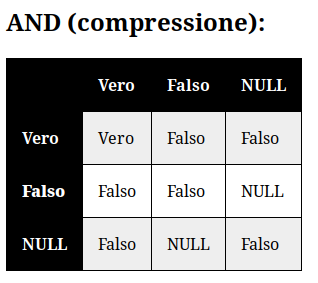
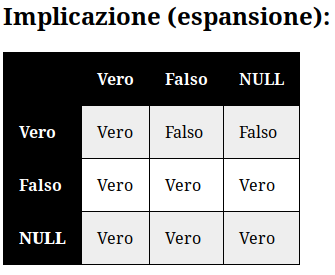
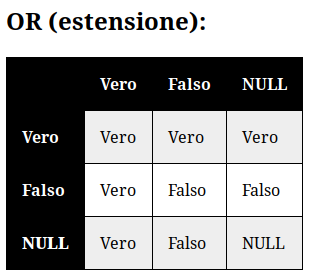
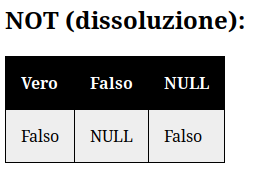

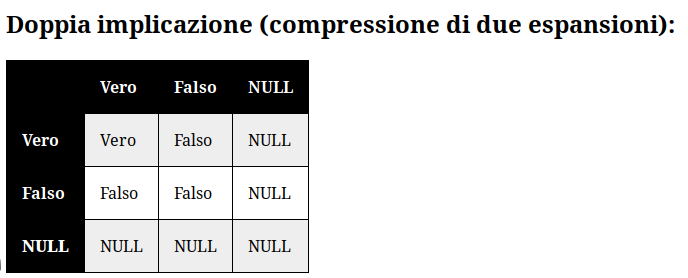
Per comodità mi sono permesso anche di scrivere un codice in python che permetta una formulazione più semplificata ed immediata delle proposizioni formali. Troverete il progetto della logica ontologica in questo repository Gitlab.

Con questo software è stato possibile oltretutto ricavare le tautologie. Parto già dal presupposto che i teoremi di De Morgan sono relativi alla logica booleana, pertanto non verranno inclusi in questa sezione. Anche perché not(not a) in logica booleana darebbe a, mentre nella logica ontologica darebbe non apofantico.
Per la legge d'identità posso dire che non fonda l'essere in quanto l'identità può essere data solo per le proprietà. È possibile dire che a e b hanno le stesse proprietà e quindi sono identici, ma questo non significa che a e b sono la stessa cosa, cioè la stessa determinazione. Il problema in filosofia è che si usa il principio di identità in ontologia affermando che l'essere sia una proprietà, cadendo poi in contraddizione. Il principio di identità serve solo a livello epistemologico per permetterci di conoscere, per sapere che per esempio una determinata configurazione di proprietèà corrisponde ad un albero di fichi e un'altra ad un albero di ciliege.
Di fatto l'ente è derivato dal principio di identità stesso a partire dalle proprietà, che potremmo chiamare anche determinati, in quanto sono termini che implicitano un aggregato di proprietà o comunque di altri determinati, messe in relazione tra di loro per mezzo della logica stessa. Possiamo infatti recuperare il principio di identità A→A come principio epistemico per mostrare come si formano gli enti a partire dai determinati, seguendo il motto di Quine "no entity without identity":
C.I.E. (criterio di identità epistemico): x è un ente se e solo se esiste un determinato y e x condivide le stesse proprietà epistemiche (K) di y. ∃x∃y|(Kx=Ky)↔x=y
dove
- x=ente
- y= determinato
- ∃= quantificatore esistenziale, si legge "esiste almeno un x"
- K= proprietà epistemiche
Per chiarezza sarebbe meglio individuare i determinati in modo diverso dagli enti, per esempio con l'alfabeto greco, seppur comunque ciò riguarda un'argomentazione ristretta che se estesa a quella formale andrebbe a porre inutili complicazioni, argomentabili benissimo dalla teoria degli enti e dei determinati. Le proprietà epistemiche sono le proprietà neurofisiologiche che ci permettono di conoscere il determinato. Questo criterio di identità epistemico permette all'io di passare dal determinato all'ente e soprattutto consente la formulazione del senso comune secondo cui è ente solo ciò che si dà nello spaziotempo. Essendo un criterio epistemico questo è solo una sorta di "criterio di traduzione" e non ci dice che gli enti abbiano verità ma solo come i determinati vengono trasformati in enti. In altre parole, la formula è un criterio di identità che permette di comprendere come un determinato tramite l'io viene ridotto ad un ente, il criterio di identità serve proprio per vedere come questo sia possibile. Attraverso le proprietà estratte dalla percezione in modo induttivo si aggiunge la sostanza dell'ente così creato in modo che esso segua quel criterio di identità epistemico. Pertanto non è un criterio usato per riconoscere i determinati ma gli enti. Gli enti esistono grazie al criterio di identità, mentre i determinati no, in quanto sono proprietà. Una sedia per esempio non esiste perché è una sedia, ma esiste come determinato dell'essere e l'ente è semplicemente la sedia in sé assunta solo nelle sue proprietà epistemiche. L'ente, ribadendo il concetto, esiste solo grazie al principio di identità. Con il principio di identità poi è possibile anche fare il processo inverso, cioè verificare se un ente postulato dalla metafisica può esistere anche come determinato, dato che la doppia implicazione si può leggere nei due sensi. La sedia esiste come determinato. Ma la sedia allo stesso tempo può essere concepita come un ente poiché da essa vengono astratte delle proprietà che provengono da una indagine epistemologica, ovvero vengono evidenziate quelle caratteristiche che attraverso una identificazione che avviene per osservazione, possano essere ricondotte al concetto di sedia. Quindi l'oggetto preso in considerazione può essere "catalogato" come sedia poiché rispetta queste condizioni epistemiche che la identificano in tale modo. Infatti tramite questo si può spiegare la formula come: esiste una sedia (l'ente preso in considerazione) poiché esiste la sedia (che consiste nel concetto di sedia determinato a priori), tale che, le caratteristiche contenute dall'ente-sedia sono condivise con il concetto di sedia che è il determinato. Questo si traduce con una equivalenza (il simbolo "↔") che si va a stabilire tra l'ente e il determinato, così che si possa giustificare la permanenza dell'ente a discapito del determinato, poiché appunto viene assunto che l'ente sia collegato tramite le sue caratteristiche a quelle del determinato. I determinati esistono dialetticamente, gli enti no. Tuttavia se si fanno opportune operazioni ad un determinato può corrispondere un ente, il determinato in questione e l'ente in questione si chiamano allo stesso modo, ciò che cambia è come vengono concepiti nella teoria. Il determinato si chiama sedia e si chiama sedia anche l'ente. Che cosa cambia? Che secondo la teoria il determinato esiste dialetticamente e quindi non esiste un criterio di identità tra determinati, perché sul piano ontologico la dialettica è proprio delle esistenze, le esistenze si danno per opposizione nei confronti del non essere. Invece sul piano epistemologico (cioè sul piano della conoscenza) è possibile prendere un determinato, astrarre le sue proprietà epistemiche e renderlo un ente. Questo è un processo nichilista, ma il criterio di identità ci serve per poter dire tante cose come:
- È falso che l'ente è identico a sé stesso, ma è al massimo identico all'astrazione delle sue proprietà epistemiche.
- Poiché la doppia implicazione si può leggere in due sensi, si può vedere se un ente postulato metafisicamente si può tradurre in un determinato, in tal caso dovrebbe essere possibile un determinato con lo stesso nome dell'ente che esiste dialetticamente.
Esempio: dio viene concepito come un ente dalla metafisica e gli vengono ascritte determinate proprietà: onnipotenza, onniscienza, creatore degli altri enti etc. E tale discorso vale all'interno della metafisica perché l'essere è (solo nella metafisica) un predicato. Se invece applichiamo il nostro criterio ci dobbiamo chiedere se può esistere un determinato con le medesime proprietà epistemiche dell'ente dio, e ci rendiamo subito conto che non è così perché nessun determinato può essere onnipotente, altrimenti risolverebbe in sé ogni altro determinato e non sarebbe possibile determinare nulla, nessun determinato può essere creato perché significherebbe che egli non è stato e quindi che deriva dal non essere, e via discorrendo. Quindi si conclude che dio esiste come ente, ma non come determinato. Ma noi sappiamo grazie all'ontologia che gli enti non hanno verità, e quindi preferiamo sistemi ontologici a sistemi metafisici. Da questo ne deriva che dio, come determinato, è ontologicamente contraddittorio.
Dunque:
- Può esiste qualcosa che abbia le medesime proprietà implicitate nel concetto di dio?
- No, poiché nessun determinato può essere onnipotente: altrimenti risolverebbe in sé ogni altro determinato e non sarebbe possibile determinare nulla.
- Nell'onnipotenza di dio non è possibile determinare nulla.
- Nulla è stato mai creato, altrimenti significherebbe che qualcosa non è mai esistita, derivando dal non essere.
- Dio esiste come ente e non come determinato, cioè come aggregato di proprietà.
- Gli enti non hanno verità perché si pongono adialetticamente e noi ci serviamo della dialettica perché possiamo conoscere i determinati solo per mezzo di essa.
- Dio ha lo statuto ontologico delle esistenze impossibili.
Noi possiamo formulare tutti gli enti che vogliamo, vedere se esistono significa partire da queste proprietà e vedere se sono dialetticamente concepibili. In un certo senso il reame metafisico è equivalente al reame della possibilità, e quindi la metafisica esiste solo come contesto modale. Tuttavia noi quando facciamo ontologia deduciamo i determinati direttamente dalla struttura dialettica, visto che sappiamo che qualsiasi ente dedotto dalla struttura modale della metafisica è necessariamente contraddittorio. Tuttavia potremmo imbatterci in un sistema e non sapere se è metafisico o ontologico, ed ecco che qui ci torna in aiuto il criterio che è stato formulato e formalizzato. Nella storia della filosofia ontologia e metafisica vengono viste come due facce della stessa medaglia, mentre nel sistema qui proposto sono contrapposte: ontologico è ciò che esiste senza contraddizioni, metafisico invece è tutto ciò che per esistere ha bisogno di un contesto modale, e quindi fonda il suo sistema sulla contraddizione che l'essere è un predicato, eliminando qualsiasi attualità dalla possibilità.
E qui si ritorna a prima: qual è la differenza tra Babbo natale e dio? Babbo natale viene concepito come una figura che deriva dai miti, quindi una figura proiettiva che può essere eliminata con la psicanalisi e non serve l'ontologia. Dio ha bisogno di entrambe per essere eliminato, perché esiste sia come mito che come ente metafisico. Quindi abbiamo due tipi di possibilità: la possibilità logica, o modale, che è ammessa all'interno della metafisica e questa si rivela sempre in impossibilità nel mondo reale, e poi c'è la possibilità epistemica che è all'interno del mondo reale, e non si può risolvere con l'ontologia, ma sono necessarie psicologia e scienza. Questo perché un determinato può essere ontologicamente possibile, e questo significa che non viola la dialettica, ma non sappiamo se l'essere si determina effettivamente in quel modo. Ad esempio non possiamo sapere senza l'ausilio della scienza se esistono le tigri verdi con le strisce viola, e di questo se ne occupa la scienza, e magari si potrebbe scoprire che con accurate mutazioni genetiche possono esistere, così come possiamo non sapere se esiste una determinata specie di batterio, di alga o di fungo e porci domande scientifiche. Così si capisce questo: anche la scienza, a suo modo, è ontologia. Ma è ontologia speciale, non generale. Essa va a caccia dei determinati e può farlo se e solo se rispetta l'ontologia qui proposta. Ad esempio la biologia è una ontologia speciale degli esseri viventi, l'informatica delle informazioni, etc. Quindi chi si occupa di scienza si occupa sempre direttamente anche di ontologia. E quindi, chi si occupa di informatica si occupa direttamente anche di ontologia, come argomentato d'altronde anche in questo articolo.
A seguire le ulteriori leggi per la logica ontologica e di conseguenza le tautologie rispettate rispetto a quelle non rispettate (ma rispettate in quella booleana). I simboli utilizzati sono ! per la negazione, v per l'OR, ^ per l'AND, - per la coimplicazione, etc. Il glossario dei simboli lo trovate nel file di configurazione presso il repository Gitlab.
Tautologie rispettate:
Modus ponens:
(A^(A→B))→B
(V^(V→V))→V = V
(V^(V→N))→N = V
(V^(V→F))→F = V
(N^(N→V))→V = V
(N^(N→N))→N = V
(N^(N→F))→F = V
(F^(F→V))→V = V
(F^(F→N))→N = V
(F^(F→F))→F = V
Modus tollens:
(!B^(A→B))→!A
(!V^(V→V))→!V = V
(!V^(N→V))→!N = V
(!V^(F→V))→!F = V
(!N^(V→N))→!V = V
(!N^(N→N))→!N = V
(!N^(F→N))→!F = V
(!F^(V→F))→!V = V
(!F^(N→F))→!N = V
(!F^(F→F))→!F = V
Sillogismo ipotetico:
((A→B)^(B→C))→(A→C)
((V→V)^(V→V))→(V→V) = V
((V→V)^(V→N))→(V→N) = V
((V→V)^(V→F))→(V→F) = V
((V→N)^(N→V))→(V→V) = V
((V→N)^(N→N))→(V→N) = V
((V→N)^(N→F))→(V→F) = V
((V→F)^(F→V))→(V→V) = V
((V→F)^(F→N))→(V→N) = V
((V→F)^(F→F))→(V→F) = V
((N→V)^(V→V))→(N→V) = V
((N→V)^(V→N))→(N→N) = V
((N→V)^(V→F))→(N→F) = V
((N→N)^(N→V))→(N→V) = V
((N→N)^(N→N))→(N→N) = V
((N→N)^(N→F))→(N→F) = V
((N→F)^(F→V))→(N→V) = V
((N→F)^(F→N))→(N→N) = V
((N→F)^(F→F))→(N→F) = V
((F→V)^(V→V))→(F→V) = V
((F→V)^(V→N))→(F→N) = V
((F→V)^(V→F))→(F→F) = V
((F→N)^(N→V))→(F→V) = V
((F→N)^(N→N))→(F→N) = V
((F→N)^(N→F))→(F→F) = V
((F→F)^(F→V))→(F→V) = V
((F→F)^(F→N))→(F→N) = V
((F→F)^(F→F))→(F→F) = V
Prima legge di pseudo Scoto:
A^!A→B
V^!V→V = V
V^!V→N = V
V^!V→F = V
N^!N→V = V
N^!N→N = V
N^!N→F = V
F^!F→V = V
F^!F→N = V
F^!F→F = V
Legge di Peirce:
((A→B)→A)→A
((V→V)→V)→V = V
((V→N)→V)→V = V
((V→F)→V)→V = V
((N→V)→N)→N = V
((N→N)→N)→N = V
((N→F)→N)→N = V
((F→V)→F)→F = V
((F→N)→F)→F = V
((F→F)→F)→F = V
Tautologie non rispettate:
Legge della doppia negazione:
(!A)-A
!(!V)-V = N
!(!N)-N = N
!(!F)-F = F
Legge di idempotenza:
AvA-A
VvV-V = V
NvN-N = N
FvF-F = F
Legge del terzo escluso: richiedeva la legge del quarto escluso.
Av!A
Vv!V = V
Nv!N = F
Fv!F = F
Principio di non contraddizione (il fatto che non sia una tautologia la rende una logica dialetista):
!(A^!A)
!(V^!V) = N
!(N^!N) = F
!(F^!F) = F
Legge di contrapposizione:
(A→B)-(!B→!A)
(V→V)-(!V→!V) = V
(V→N)-(!N→!V) = F
(V→F)-(!F→!V) = F
(N→V)-(!V→!N) = V
(N→N)-(!N→!N) = V
(N→F)-(!F→!N) = V
(F→V)-(!V→!F) = V
(F→N)-(!N→!F) = V
(F→F)-(!F→!F) = V
Propietà associativa di AND:
A^(B^C)-(A^B)^C
V^(V^V)-(V^V)^V = V
V^(V^N)-(V^V)^N = F
V^(V^F)-(V^V)^F = F
V^(N^V)-(V^N)^V = F
V^(N^N)-(V^N)^N = F
V^(N^F)-(V^N)^F = F
V^(F^V)-(V^F)^V = F
V^(F^N)-(V^F)^N = F
V^(F^F)-(V^F)^F = F
N^(V^V)-(N^V)^V = F
N^(V^N)-(N^V)^N = N
N^(V^F)-(N^V)^F = N
N^(N^V)-(N^N)^V = N
N^(N^N)-(N^N)^N = N
N^(N^F)-(N^N)^F = F
N^(F^V)-(N^F)^V = N
N^(F^N)-(N^F)^N = F
N^(F^F)-(N^F)^F = N
F^(V^V)-(F^V)^V = F
F^(V^N)-(F^V)^N = F
F^(V^F)-(F^V)^F = F
F^(N^V)-(F^N)^V = F
F^(N^N)-(F^N)^N = F
F^(N^F)-(F^N)^F = N
F^(F^V)-(F^F)^V = F
F^(F^N)-(F^F)^N = N
F^(F^F)-(F^F)^F = F
Proprietà associativa di OR:
Av(BvC)-(AvB)vC
Vv(VvV)-(VvV)vV = V
Vv(VvN)-(VvV)vN = V
Vv(VvF)-(VvV)vF = V
Vv(NvV)-(VvN)vV = V
Vv(NvN)-(VvN)vN = V
Vv(NvF)-(VvN)vF = V
Vv(FvV)-(VvF)vV = V
Vv(FvN)-(VvF)vN = V
Vv(FvF)-(VvF)vF = V
Nv(VvV)-(NvV)vV = V
Nv(VvN)-(NvV)vN = V
Nv(VvF)-(NvV)vF = V
Nv(NvV)-(NvN)vV = V
Nv(NvN)-(NvN)vN = N
Nv(NvF)-(NvN)vF = F
Nv(FvV)-(NvF)vV = V
Nv(FvN)-(NvF)vN = F
Nv(FvF)-(NvF)vF = F
Fv(VvV)-(FvV)vV = V
Fv(VvN)-(FvV)vN = V
Fv(VvF)-(FvV)vF = V
Fv(NvV)-(FvN)vV = V
Fv(NvN)-(FvN)vN = F
Fv(NvF)-(FvN)vF = F
Fv(FvV)-(FvF)vV = V
Fv(FvN)-(FvF)vN = F
Fv(FvF)-(FvF)vF = F
Proprietà commutativa di AND:
A^B-B^A
V^V-V^V = V
V^N-N^V = F
V^F-F^V = F
N^V-V^N = F
N^N-N^N = F
N^F-F^N = N
F^V-V^F = F
F^N-N^F = N
F^F-F^F = F
Proprietà commutativa di OR:
AvB-BvA
VvV-VvV = V
VvN-NvV = V
VvF-FvV = V
NvV-VvN = V
NvN-NvN = N
NvF-FvN = F
FvV-VvF = V
FvN-NvF = F
FvF-FvF = F
Proprietà distributiva della congiunzione rispetto alla disgiunzione:
A^(BvC)-(A^B)v(B^C)
V^(VvV)-(V^V)v(V^V) = V
V^(VvN)-(V^V)v(V^N) = V
V^(VvF)-(V^V)v(V^F) = V
V^(NvV)-(V^N)v(N^V) = F
V^(NvN)-(V^N)v(N^N) = F
V^(NvF)-(V^N)v(N^F) = F
V^(FvV)-(V^F)v(F^V) = F
V^(FvN)-(V^F)v(F^N) = F
V^(FvF)-(V^F)v(F^F) = F
N^(VvV)-(N^V)v(V^V) = V
N^(VvN)-(N^V)v(V^N) = F
N^(VvF)-(N^V)v(V^F) = F
N^(NvV)-(N^N)v(N^V) = F
N^(NvN)-(N^N)v(N^N) = F
N^(NvF)-(N^N)v(N^F) = N
N^(FvV)-(N^F)v(F^V) = F
N^(FvN)-(N^F)v(F^N) = N
N^(FvF)-(N^F)v(F^F) = F
F^(VvV)-(F^V)v(V^V) = V
F^(VvN)-(F^V)v(V^N) = F
F^(VvF)-(F^V)v(V^F) = F
F^(NvV)-(F^N)v(N^V) = F
F^(NvN)-(F^N)v(N^N) = F
F^(NvF)-(F^N)v(N^F) = N
F^(FvV)-(F^F)v(F^V) = F
F^(FvN)-(F^F)v(F^N) = F
F^(FvF)-(F^F)v(F^F) = F
Proprietà distributiva della disgiunzione rispetto alla congiunzione:
Av(B^C)-(AvB)^(BvC)
Vv(V^V)-(VvV)^(VvV) = V
Vv(V^N)-(VvV)^(VvN) = V
Vv(V^F)-(VvV)^(VvF) = V
Vv(N^V)-(VvN)^(NvV) = V
Vv(N^N)-(VvN)^(NvN) = F
Vv(N^F)-(VvN)^(NvF) = F
Vv(F^V)-(VvF)^(FvV) = V
Vv(F^N)-(VvF)^(FvN) = F
Vv(F^F)-(VvF)^(FvF) = F
Nv(V^V)-(NvV)^(VvV) = V
Nv(V^N)-(NvV)^(VvN) = F
Nv(V^F)-(NvV)^(VvF) = F
Nv(N^V)-(NvN)^(NvV) = F
Nv(N^N)-(NvN)^(NvN) = F
Nv(N^F)-(NvN)^(NvF) = N
Nv(F^V)-(NvF)^(FvV) = F
Nv(F^N)-(NvF)^(FvN) = N
Nv(F^F)-(NvF)^(FvF) = F
Fv(V^V)-(FvV)^(VvV) = V
Fv(V^N)-(FvV)^(VvN) = F
Fv(V^F)-(FvV)^(VvF) = F
Fv(N^V)-(FvN)^(NvV) = F
Fv(N^N)-(FvN)^(NvN) = N
Fv(N^F)-(FvN)^(NvF) = F
Fv(F^V)-(FvF)^(FvV) = F
Fv(F^N)-(FvF)^(FvN) = F
Fv(F^F)-(FvF)^(FvF) = F
Seconda legge di pseudo Scoto:
A→(!A^B)
V→(!V^V) = F
V→(!V^N) = F
V→(!V^F) = F
N→(!N^V) = V
N→(!N^N) = V
N→(!N^F) = V
F→(!F^V) = V
F→(!F^N) = V
F→(!F^F) = V
Prima legge di De Morgan:
A^B-!(!A^!B)
V^V-!(!V^!V) = N
V^N-!(!V^!N) = N
V^F-!(!V^!F) = F
N^V-!(!N^!V) = N
N^N-!(!N^!N) = N
N^F-!(!N^!F) = N
F^V-!(!F^!V) = F
F^N-!(!F^!N) = N
F^F-!(!F^!F) = N
Seconda legge di De Morgan:
AvB-!(!Av!B)
VvV-!(!Vv!V) = N
VvN-!(!Vv!N) = N
VvF-!(!Vv!F) = N
NvV-!(!Nv!V) = N
NvN-!(!Nv!N) = N
NvF-!(!Nv!F) = N
FvV-!(!Fv!V) = N
FvN-!(!Fv!N) = N
FvF-!(!Fv!F) = F
Consequentia mirabilis:
(!A→A)→A
(!V→V)→V = V
(!N→N)→N = F
(!F→F)→F = F
Rimarrebbero da definire la compattezza, la completezza, la correttezza, la sensatezza, la decidibilità, l'adeguatezza, i teoremi di limite, la conservatività, l'efficienza, la chisura sotto operazioni e la struttura modale di questa logica ontologica, ma rimando al futuro l'analisi di queste proprietà, in quanto richiedono approfondimenti che ora non si rendono necessari.
Nel prossimo articolo tratteremo le proprietà e inizieremo a fare correlazioni tra lingua italiana ed espressione formale nella logica ontologica predicativa.
![Clean Code: L’Economia dei Commenti [4/12]](/uploads/Clean_Code4_of_12_SORINT_lab_b2c605d6bf.png)


![Clean Code: Manuale per un Codice di Qualità [1/12]](/storage/media/fb9d400303282148ed861968781dbe8c/2-Code_like_SORINTian_Clean_SORINT.lab.png)



